Summer is right around the corner and it is time to spend more time outdoors. Shocking, I know, but after enduring yet another German Winter™ it is just such a relief to go outside and actually get some sun and see nature alive again. Colors! Scents! Not feeling like the day has ended at 5pm, what a joy! To celebrate this, my friends and I wanted to tackle some projects in our garden. There is this old shelter that has been slowly rotting away and which we want to fix. Like with software, the best fix is a rewrite, so we decided to rip everything out and build a new shelter! Not that I have any experience in building (or even planning) shelters, but how hard can it be? (Spoiler: The math was hard!)

We wanted to stick with the current layout, just expand it a bit. It is basically a slanted roof on top of some beams, pretty standard I guess. There is also an old construction trailer with a leaky roof sitting right next to the shelter, so we decided to expand the shelter to cover the trailer as well. I remembered my university days where I did some 3D modeling and though: "I can plan this in 3D!" Sadly I don't have cheap access to high-end modeling software anymore, but SketchUp is free and I decided to give it a try. Here is what I came up with:

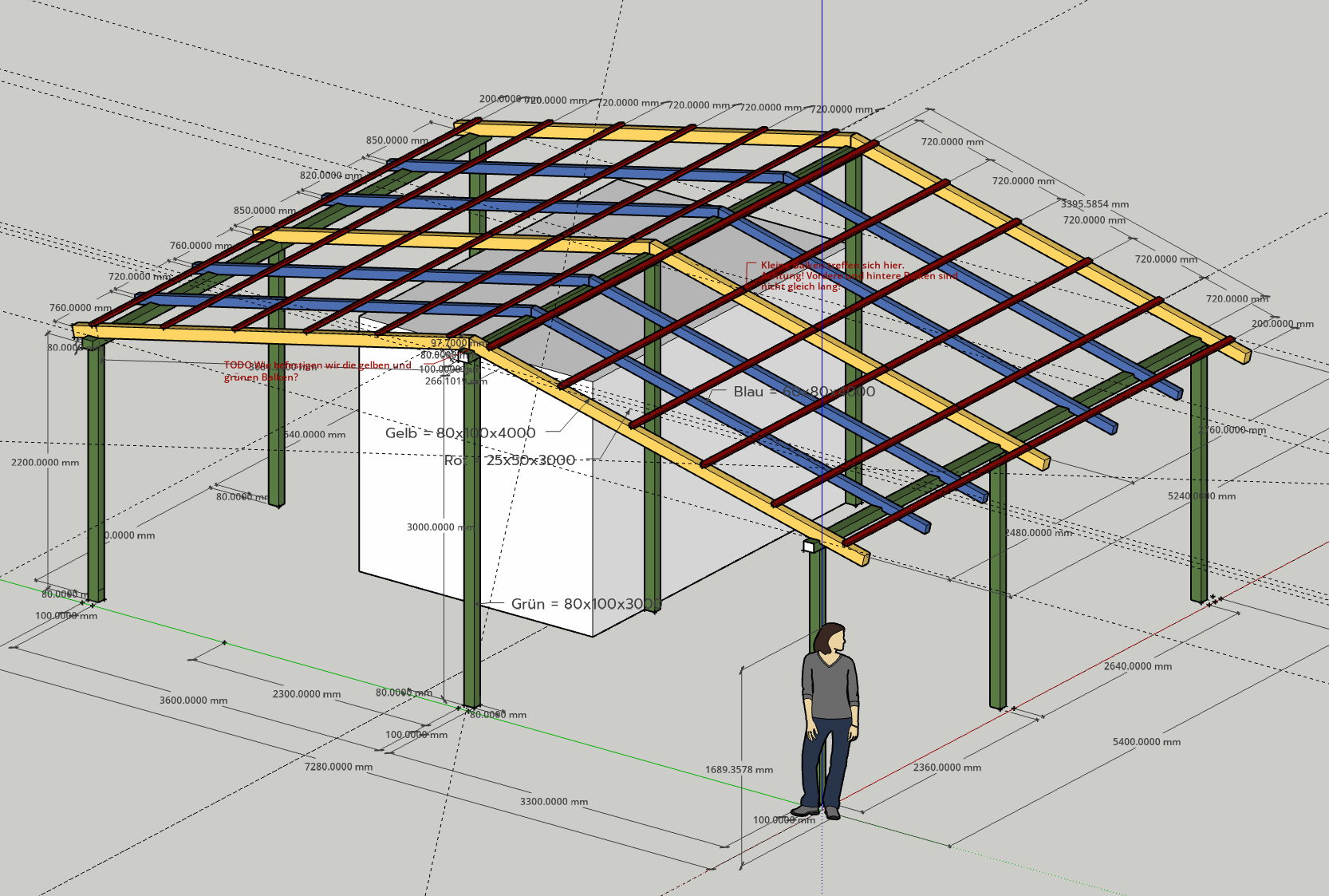
Picture of my 3D model of the new shelter, two slanted roofs on top of some wooden beams

There might be some small structures missing here and there, but overall I am happy with it. There was just one small hiccup. Notice the yellow beams meeting on top of the middle green beam? Here is a closeup:

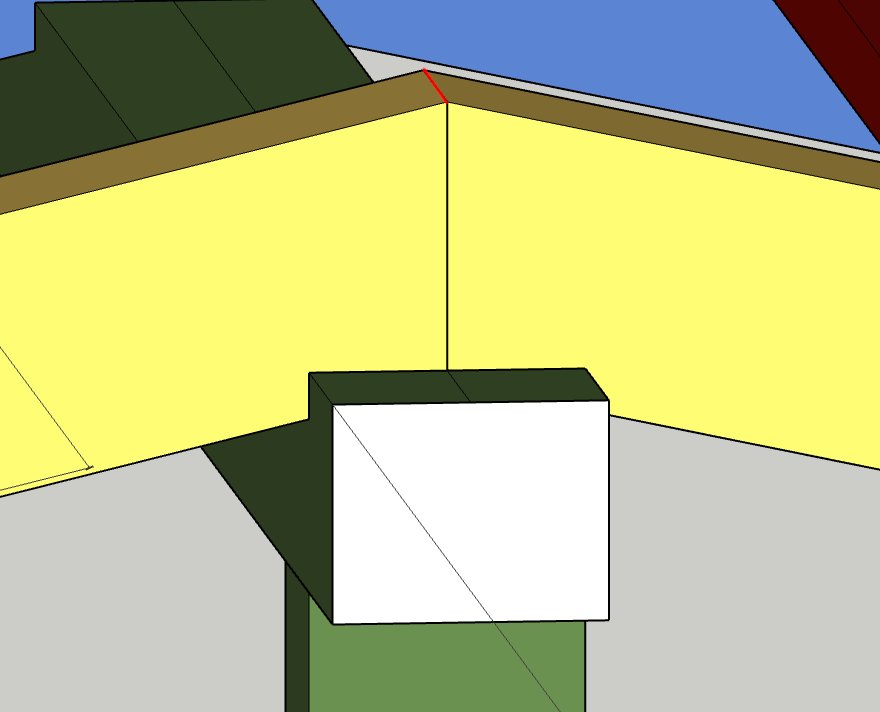
Closeup of the joint of the main beams that will carry the roof tiling. It has an interesting geometry

I wanted to construct the 3D model with exactly the right proportions to use it as a reference, taking into account the type of wood that we will be using. The yellow beams are 80x100x4000mm beams slanted at an angle, and I wanted them to meet in this nice "hat-shape". Turns out this exists and is called a "Pfattendach" in German, but of course I didn't know that when I designed the roof and was too lazy to look up existing roof structures. The design process was so much fun that it sucked me right in and I wanted to figure everything out for myself.

Here is where it got intersting, because I stumbled upon a unexpectedly tricky bit of math that took me way too long to crack. In the first picture, notice that the yellow beams are slanted due to the height difference between the middle pillar and the outer pillars (the vertical green beams). The middle pillar is 3000mm high, the outer pillars are 2200mm high, so a height difference of 800mm. To reduce waste, I wanted the yellow beams to rest with one of their short edges right above the middle of the middle pillar (see the red line in the second image). Since the yellow beams are slanted, I now had to figure out two things:

The slant angle
The exact dimensions of the shape to cut out of the yellow beam so the red edge rests exactly in the middle

To simplify, here is a 2D picture illustrating the situation:

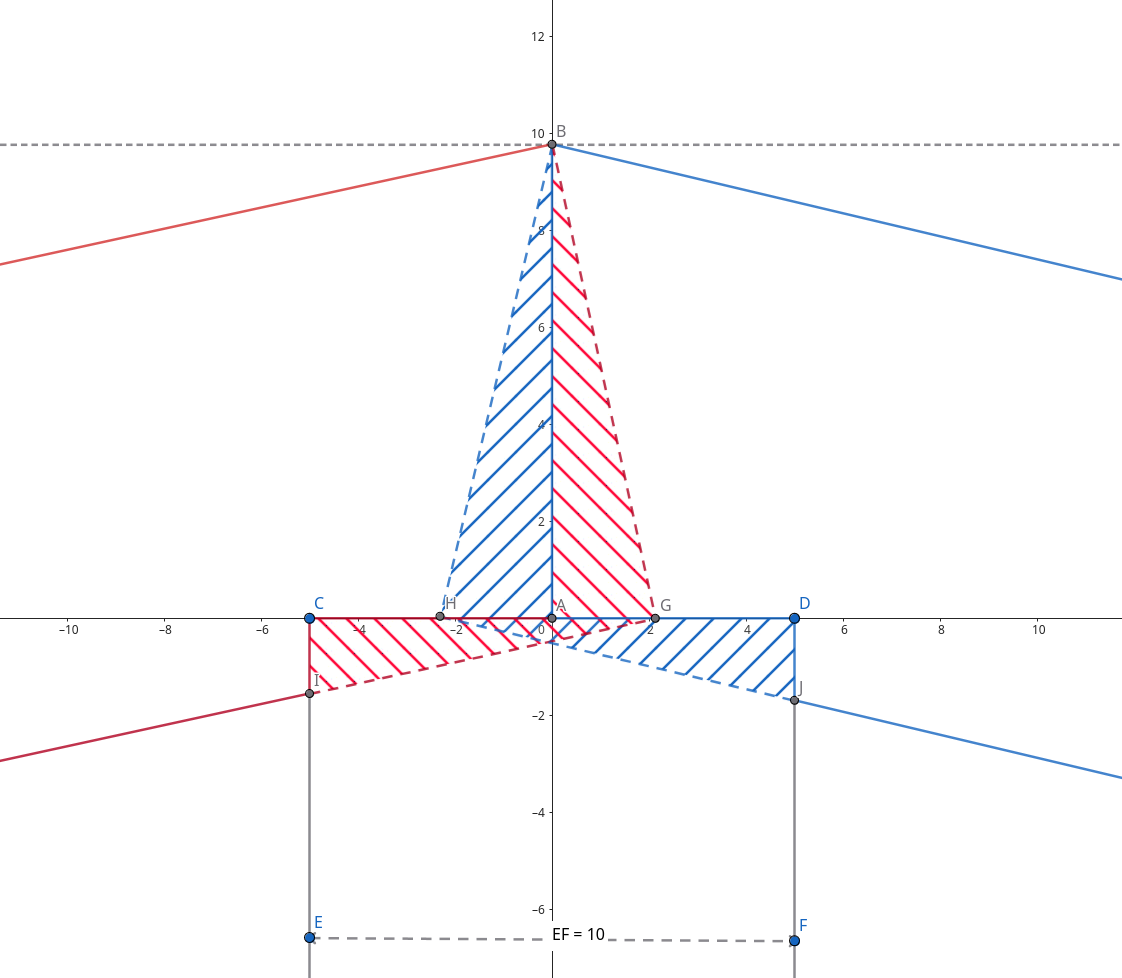
2D schematic of the yellow beams and their joint

The cross-hatched areas are what we have to cut out of the beams. The point B is the red edge from the previous picture and marks one of the ends of the beams. I basically pivot the whole beam around this edge. The red dashed line between B and G is the end of the beam. Notice how G (the opposite edge of B) is a bit offset from the center point A? The question is: By how much?

At this point I thought that this would be easy. Just a bit of trigonometry and Pythagoras' Theorem. It still looks a bit complicated, so I simplified the problem even further to this:

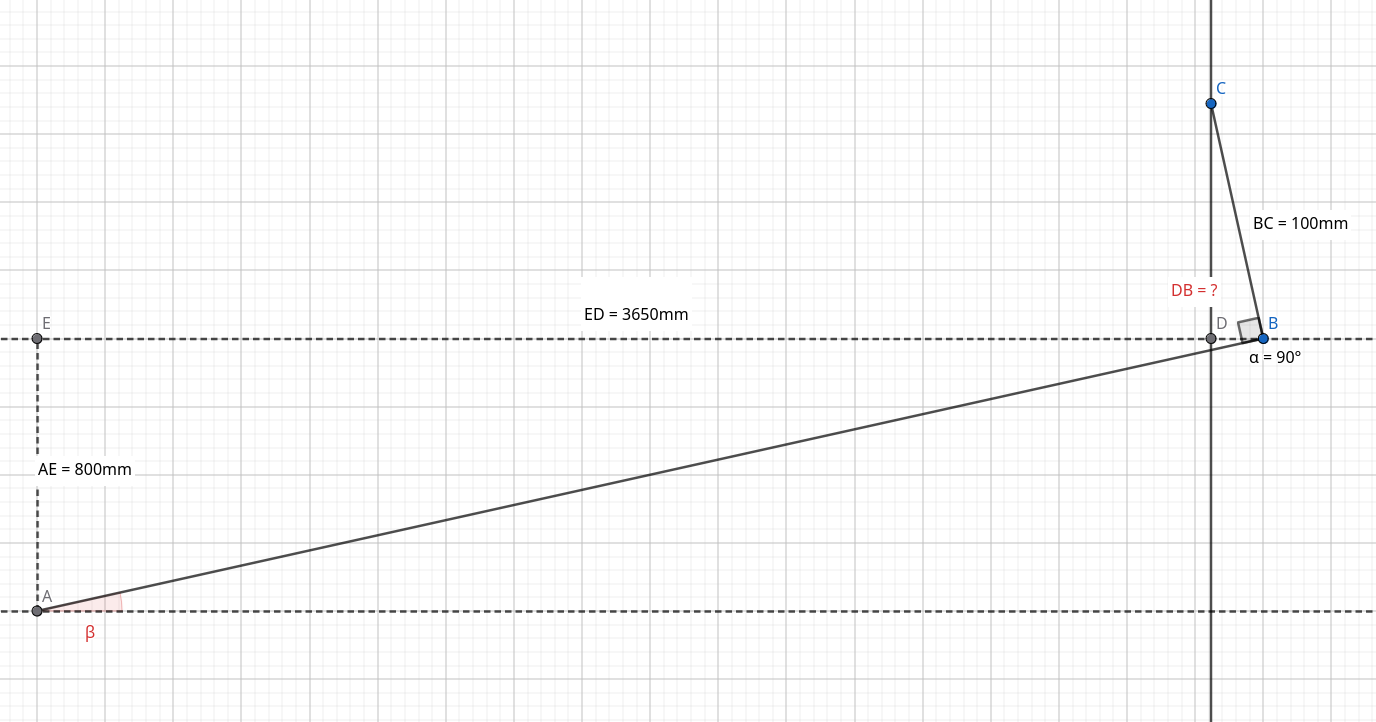
The simplest version of my roof-beam-problem

First, the measurements: $\overline{AE}=800mm$ , that is just the height difference of the pillars. $\overline{ED}=3650mm=3600mm+\frac{100mm}{2}$ is the horizontal distance between the pillars, plus half the width of the middle pillar (again an 80x100x4000mm beam, with the 100mm side facing us). $\overline{BC}=100mm$ is the same beam width.

Now we look for the angle β and the distance $\overline{DB}$ (or alternatively $\overline{CD}$ ). If you want to take a shot at the problem yourself, pause here and try it out. Maybe you'll find it much less difficult than I did :)

Before I show my solution, I want to illustrate what exactly made this problem difficult for me!

Unexpected difficulties

At first glance, it looks like we should be able to solve this easily. We know $\overline{AE}$ and $\overline{ED}$ , so we can get the length of the diagonal line... But wait, the diagonal is $\overline{AB}$ and not $\overline{AD}$ ... Ok then maybe we can do something with the small triangle? But there we don't know $\overline{CD}$ and $\overline{DB}$ and also don't know the angle between $\overline{CD}$ and $\overline{CB}$ . We could try to add a new point where $\overline{AB}$ meets the extension of $\overline{CD}$ to get a different triangle, but then we still don't have enough information.

I played around with it some more, but everytime I ended up with equations that had too many undefined variables. Funnily enough, I showed ChatGPT the last image (using the o4-mini model) and it processed for 5 minutes and then crashed. With some additional explanation it eventually figured it out, but solving geometry problems from images doesn't seem to be its strong suite.

So here is my solution that I eventually found, showing why it it just a bit more complicated than I anticipated.

My solution

So I was on the right track all along: No single triangle is enough to solve this. The two most promising equations are these (using $d$ for $\overline{DB}$ and dropping the units for readability):

\begin{align} \tag{1} \tan{\beta}=\frac{800}{3650+d} \end{align}

\begin{align} \tag{2} \sin{\beta}=\frac{d}{100} \end{align}

Equation (1) describes the big triangle, equation (2) the little triangle. We can reorder (2) in terms of $\beta$ and put it in (1) to get this:

\begin{align} \tag{3} \tan{\arcsin{\frac{d}{100}}}=\frac{800}{3650+d} \end{align}

At this point my trigonometry knowledge left me, because I though $\tan{\arcsin{x}}$ looked just a bit too scary to solve. Turns out, there is a trigonometric identity for exactly this statement, and it surprised me a bit:

\begin{align} \tag{4} \tan{\arcsin{x}}=\frac{x}{\sqrt{1-x^2}} \end{align}

To be fair, you have to scroll quite a bit on Wikipedia to find it, but it looks surprisingly clean. With that, we can rearrange our equation, substituting $x=\frac{d}{100}$ :

\begin{align} \tag{5} \frac{\frac{d}{100}}{\sqrt{1-(\frac{d}{100})^2}}=\frac{800}{3650+d} \end{align}

First we can resolve the triple-fraction on the left side, by bringing the $100mm$ down and into the square-root, where it cancels out the inner denominator and leaves us with this:

\begin{align} \tag{6} \frac{d}{\sqrt{10000-d^2}}=\frac{800}{3650+d} \end{align}

Now we multiply with the denominators of both fractions and get this:

\begin{align} \tag{7} d3650+d^2=800(\sqrt{10000-d^2}) \end{align}

Now we have to square to get rid of the square-root:

\begin{align} \tag{8} (d3650+d^2)^2=800^2(10000-d^2) \end{align}

This is a fourth-degree polynomial! Why is there a fourth-degree polynomial in my beautiful roof design?! Let's reorder it to look at it in all its glory:

\begin{align} \tag{9} d^4+7.300d^3+13.962.500d^2-6.4*10^9=0 \end{align}

I certainly wouldn't have imagined that I would have to solve such a complicated polynomial to find $\beta$ and $d$ . And to be fair, I didn't solve it by hand, WolframAlpha did it for me. Funnily enough, fourth-degree polynomials are the highest degree of polynomials that even have a formula for finding the roots. Even then, the formula (called the quartic formula) is super complicated. Don't believe me? Take a look at this monstrosity:

The quartic formula

So here we are, we found a formula for finding $d$ . We already know how to calculate $\beta$ from $d$ (using equation (2) for example), so we end up with these values:

d=21.29mm

\beta=12.29°

Bonus round - The two roofs are not symmetrical

There is a bonus problem: Our two roofs are not symmetrical! We did the calculation for one side, where the horizontal distance between the pillars is 3600mm, but on the other side, due to an annoying fence, the pillars are closer together (3300mm to be precise). Take a look at this picture again:

2D schematic of the yellow beams and their joint

If you look closely (like, really closely), you will notice that $\overline{AG}$ is not the same as $\overline{AH}$ , because the blue beam is at a slightly different angle than the red beam. If you zoom in, you will actually see that the point $H$ is not even on the line $AC$ , but slightly above it! As a consequence, the line $DJ$ is a tiny bit shorter than it would be using our calculation. This is because at the new angle of the blue beam, its top edge would actually lie a bit lower than point $B$ , but since we want everything to align nicely, we have to offset that missing distance with a more shallow cut at line $DJ$ .

If you want, you can try to figure out a new adjusted formula for that, I cheated a bit and did it geometrically in SketchUp. The height difference is less than a millimeter though, so we can't saw that precisely anyway. But mathematically, there is a difference :)

Polynomial Roofs - How hard can it be to design a wooden roof?

Unexpected difficulties

My solution

Bonus round - The two roofs are not symmetrical