4.1. Product types, sum types, and the Option type
In this chapter, we will learn about optional types and the various ways we can represent such optional types using the type system. Here we will learn about the difference between product types and sum types, two concepts from the domain of functional programming.
The story of null
To understand what optional types are and why we should care, we will look at one of the most common and yet controversial concepts of computer science: null. Many programming languages support null as a concept to refer to some value that does not exist. In C this is realized through pointers with the value 0, C++ introduced a dedicated nullptr type, Java and C# have null, JavaScript even has two similar types null and undefined. If it is such a common feature, surely it is a great feature then?
From the authors personal experience, one of the more frustrating things while learning programming was dealing with null. Some languages are able to detect null values, for example Java or C#, other languages such as C and C++ just go into undefined behaviour mode where anything can happen. Checking for null values is something that was taught as an exercise in discipline to young programmers: You just have to learn to always check for null! Here is a small piece of code showing a situation where we 'forgot' to check for null:
#include <iostream>
void foo(int* ptr) {
std::cout << *ptr << std::endl;
}
int main() {
int bar = 42;
foo(&bar);
foo(nullptr);
return 0;
}
In a language that does not detect null values automatically, you are punished harshly for forgetting to check for null values, oftentimes resulting in a long and frustrating search for the reason of a program crash. But surely that's just what you get for not being disciplined enough, right? Over the history of programming, it has been shown time and again that relying on the infallability of humans is a bad idea. We make mistakes, that is just to be expected. After all, one of the main reasons why we even invented computers is so that they can do tedious calculations without making mistakes. In fact, many of the mechanisms built into programming languages are there to prevent common mistakes. Functions and variables in C, for example, automatically generate the correct code for managing stack memory, so that we as programmers don't have to do this by hand. So why should null be any different? Even the creator of the null concept, Tony Hoare, considers null to have been a bad idea, calling it his billion dollar mistake.
The problem with null is that it is a silent state. Think about a pointer type such as int*. In C, which does not know the concept of references, we have to use pointers to pass around references to other data. So we use a pointer type to tell a function: 'Here is a variable that lies at some other memory location.' So we use pointers for indirection. However pointers can be null, so suddenly, we have some added semantics that silently crept into our code: 'Here is a variable that lies at some other memory location or maybe nothing at all!' We never explicitly said that we want to pass something or nothing to the function, it is just a side-effect of how pointers work.
What is null, actually?
To get to the heart of why null can be frustrating to use, we have to understand what null actually represents. From a systems-level point of view, null is often equivalent to a null pointer, that is a pointer which points to the memory address 0x0. It has come to mean nothing over time, but nothing is a bit weird. Clearly a pointer with value 0x0 is not nothing, we just use it as a flag to indicate that a variable holds no content. There are multiple situations where this is useful:
- Indicating that something has not been initialized yet
- Optional parameters for functions or optional members in types
- Return values of functions for parameters that the function was not defined for (e.g. what is the return value of
log(0)?)
So already we see a bit of misuse here: We hijacked some special value from the domain of all values that a pointer can take, and declared that this value refers to the absence of a valueIf you think about it, why would the address 0x0 even be an invalid memory address? In a physical address space, it would be perfectly reasonable to start using memory from the beginning of the address space, so starting from the location 0x0. There are some systems where reading from and writing to 0x0 is valid, but nowadays with virtual addressing, 0x0 is generally assumed to be an invalid address for programs to access. The C standard explicitly defines that the value 0 corresponds to the null-pointer constant.. It would be better if we could separate the domain of possible memory addresses from the concept of a 'nothing' value. In the JavaScript language, there is the special undefined type, which is an attempt at encoding the absence of a value into a type. But since JavaScript is dynamically typed, forgetting to check for the presence of undefined is as real a possibility as checking for null is in other languages. But it should be possible to implement a special 'nothing' type in a statically typed programming language as well!
The main problems with null
To summarize, the two main problems with null are:
- It (silently) infiltrates a seemingly unrelated type (e.g. pointer types) and adds the concept of the absence of a value to this type
- The type system does not force us to handle
nullvalues
Think about what the first point means in C for a moment. We used pointers for a specific task, namely indirection, and now have to deal with a second concept (absence of a value) as well, even if we don't need this second concept! Conversely, if we want to indicate the absence of a value, for example in the return value of log(0), we would have to use a pointer type. Which doesn't make sense, the value 0 might be invalid for a pointer but is certainly valid as a return value of the logarithm function (log(1) == 0). What we would like instead is a special way to indicate that a value can either be some valid value, or 'nothing'.
Regarding the second problem: There is no way for the type system to know whether a pointer is null or not, and hence the compiler can't force us check for this situation. The whole point of a statically-typed language was that the compiler checks certain invariants on types for us. So why couldn't we have a language that forces us to check for the presence of null, for example like this:
void foo(int* ptr) {
deref ptr {
nullptr => return;
int& derefed => std::cout << derefed << std::endl;
}
}
It is possible to achieve something like this, and several modern programming languages already actually abandoned null for something better. In the next sections, we will understand how to build such a type form the ground up, and will see how such a type is a central part of the Rust programming language.
Using the type system to encode the absence of a value
To achieve our goal of replacing null with something better, we have to understand types a bit better. In chapter 2.3 we learned that types were these special properties that get assigned to your code that the compiler can use to enforce rules on your code (e.g. we can only assign variables with matching types to each other). This hand-wavy definition was enough to explain what a compiler does, but to build our own null-replacement, we need more knowledge.
Like most things in computer science, types come from the domain of math. A type is essentially a set: If defines the range of all possible values that a value of this type can take. A simple example for types are numbers: The number 5 is a natural number, because it is part of the set of natural numbers \( \mathbb{N} \), so we could say that the type of 5 is 'natural number'.
The number \( \frac{3}{8} \) is not part of \( \mathbb{N} \), so it's type can't be 'natural number'. Instead, it comes from the set of rational numbers (\( \mathbb{Q} \)), so it has the type 'rational number'. What the type system now does is to enforce set membership, that is to say it checks that a value declared as type A actually belongs to the set of values that A defines. So if we have the following pseudo-code:
NaturalNumber nn = 4.8;
It is the job of the type system and compiler to check whether the value 4.8 belongs to the type NaturalNumber. In this case, it does not, so an error could be raised by the compiler.
Moving to the domain of actual programming languages, we can look at some primitive types to understand how the type system treats them. The Rust-type bool, for example, is represented by the set \( \{ true, false \} \). As another example, the Rust type u8 is represented by the set \( \{ 0, 1, ..., 255 \} \). For all primitive types, these sets of valid values are well defined and relatively easy to figure out. You can try for yourself:
Exercise 4.1: What are the sets that belong to the primitive types i8, u32 and f32 in Rust? What about void* on a 64-bit system in C++? (Hint: f32 is a bit special, how does it relate to the set of real numbers \( \mathbb{R} \)?)
So what about more complex types, such as std::string in C++ or Vec<T> in Rust? We call these types composite types, because they are composed (i.e. made up of) zero or more primitive types. The builtin features for creating composite types are the struct and class keywords in C++ and the struct and enum keywords in Rust. Disregarding the enum keyword for now, both struct and class in C++ and Rust can be used to group primitive types (or other composite types) together into composite types. An interesting property of composite types can be observed now: Since all primitive types are described by finite sets, all composite types are also described by finite sets. That is to say: There are only finitely many possible values for any possible composite type. Which might seem unintuitive at first: Clearly, a type like std::string can store any possible string (disregarding memory capacity). We could store the textual representation of any natural number in a std::string, and we know there are infinitely many natural numbers. So the set of all values for the type std::string should be inifinitely large!
Our misconception here comes from the fact that we confuse the array of character values that make up the string with the actual value of type std::string. A trivial definition of the std::string type might look like this:
struct string {
char* characters;
size_t length;
};
It is composed of a pointer to the characters array, potentially allocated on the heap, as well as an integer value for the length of the stringsize_t is an unsigned integer value as big as a pointer on the target machine. On a 64-bit system, it might be equivalent to the type unsigned long long, which is 8 bytes large.. A value of this type string will be 16 bytes large in memory on a 64-bit system. Irregardless of what data the characters pointer points to, the string value itself is always just a pointer and an integer. Since they make up 16 bytes, there are \( 2^{128} \) possible values for the string type, which is a large but finite number. To check if a value matches the type string, the compiler only has to check if the value in question is made up of one value from the set of all values dictated by the char* type, and one value from the set of all values dictated by the size_t type. Note that the trick with using the size of a type to determine the number of possible values is not strictly correct. Look at the following type in Rust:
#![allow(unused)] fn main() { struct Foo { a: u32, b: bool, } }
Due to memory alignment, this type will probably be 8 bytes large. Even if we use the packed representation, the type will take 5 bytes, but not all of these bytes are actually relevant to the type. Since the b member is of type bool, the only two values it can take are true and false, for which we need only one bit instead of one byte. Using the size of the type, it would indicate that there are \( 2^{(32+8)} \) possible values, when in fact there are only \( 2^{(32 + 1)} \) possible values. So we need a different formula to determine the number of valid values for a type.
We can try to enumerate the possible values of the Foo type and try to deduce something from this enumeration. If we represent Foo as a tuple struct, it gets a bit easier to enumerate the possible values:
#![allow(unused)] fn main() { struct Foo(u32, bool); }
The possible values of Foo are: (0, false), (0, true), (1, false), (1, true), ..., (4294967295, false), (4294967295, true). For every possible value of the u32 type, there are two possible values of Foo, because bool has two possible values. So we multiply the number of possible values for each type together to obtain the number of possible values of the composite type. The mathematical operation which corresponds to this is the cross-product, since the set of all possible values of the composite Foo type is equal to the cross-product of the set of values of u32 and the set of values of bool. For this reason, we call structs in Rust and structs/classes in C++ product types.
Now, where does null come in? We already decided that we need a type that indicates the absence of a value, and we want to be able to 'glue' this type onto other types. So for example for a log function that computes a logarithm, the return value would be a floating-point number, or nothing if the value 0 was passed to log. Since it is a bit hard to enumerate all possible floating-point numbers, we will assume that the log function returns a natural number as an i32 value instead. If we enumerate the possible return values of this function, we get this set: -2147483648, ..., -1, 0, 1, ..., 2147483647, Nothing. We used a special value named Nothing to indicate the absence of a value. How could we define a type whose set of valid values is equal to this set? We could try a struct:
#![allow(unused)] fn main() { struct Nothing; struct I32OrNothing { val: i32, nothing: Nothing, } }
But we already learned that structs are product types, so the set of possible values for I32OrNothing is this: (-2147483648, Nothing), ..., (-1, Nothing), (0, Nothing), (1, Nothing), ..., (2147483647, Nothing). Not what we want! When we declare a struct with two members of type A and B in Rust (or C++), what we tell the compiler is that we want a new type that stores one value of type AAND one value of type B. To use our I32OrNothing type, we instead want a value of type i32 OR a value of type Nothing! So cleary a struct is not the right concept for this.
Enter sum types
Where with structs, we defined new types whose sets were obtained as the product of the sets of its members, we now want a type whose set of values is the sum of the set of possible values of its members. Rust supports such types with the enum keyword, and these types are aptly named sum types. C++ sadly does not support sum types, but we will see in a bit what we can do about that, for now we will work with what Rust gives us!
enums in Rust work by declaring zero or more variants. These variants define possible values of the type. enum is actually a shorthand for enumeration, and many languages support enumerations, but only a few support enumerations that are as powerful as the ones in Rust. C++ supports enumerations, but here they are simply primitive types (integer types to be exact) with a restricted set of values. So where the unsigned int type in C++ might take values from the set {0, 1, ..., 2^32-1}, with an enum in C++ we can restrict this set to specific named values:
enum class Planet {
MERCURY = 0,
VENUS = 1,
EARTH = 2,
MARS = 3,
JUPITER = 4,
SATURN = 5,
URANUS = 6,
NEPTUNE = 7,
};
The Planet type is in principle identical to the unsigned int type, but its valid set of values is smaller: {0,1,...,7}. By defining an enum, we state that any variable of this enum type will always contain exactly one of the stated variants (MERCURY, VENUS etc.). What we can't do in C++ is to have one value be of type unsigned int and another value be of another type, such as float or even a non-primitive type such as std::string. In Rust however, this is possible! So in Rust, we can define a variant that contains another type:
#![allow(unused)] fn main() { enum U8OrNone { Number(u8), NoNumber(Nothing), } }
The set of values of this type would be: {Number(0), Number(1), ..., Number(255), NoNumber(None)}. Our Nothing type now looks a bit redundant, we can actually use an empty variant for this:
#![allow(unused)] fn main() { enum U8OrNone { Number(u8), None, } }
The neat thing about enums in Rust is that they are full-fledged types, so the compiler will enforce all its type rules on variables of enum types. In particular, the compiler knows about all the possible variants and forces us to handle them. Let's look at an example in practice:
fn add_one(number: U8OrNone) -> U8OrNone { match number { U8OrNone::Number(num) => U8OrNone::Number(num + 1), U8OrNone::None => U8OrNone::None, } } fn main() { let num = U8OrNone::Number(42); let no_num = U8OrNone::None; println!("{:?}", add_one(num)); println!("{:?}", add_one(no_num)); }
Using an enum in Rust is done through pattern matching using the built-in match construct: You match on a value of an enum and provide one match arm for each of the possible variants. The match arms are structured like this: variant => statement, where variant is one of the variants and statement can be any statement. Perhaps most interestingly, we can get access to the internal data of a variant inside a match arm: U8OrNone::Number(num) gives a name (num) to the value inside the Number(u8) variant, and we can work with this value. In this case, we write a function that takes a number or nothing and try to add one to the number. If there is no number, we simply return None, but if there is a number, we unpack the value using the match arm, add one to it and pack it back into another U8OrNone.
Notice how we never could have forgotten that there is a special None value here? Because we encoded this value into a type, the compiler enforced us to handle this special value! This is much better than null, which was part of a types value set silently. If we try to use the U8OrNone type directly, for example to add a value to it, we get a compile error:
#![allow(unused)] fn main() { fn add_one_invalid(number: U8OrNothing) -> U8OrNothing { number + 1 } }
error[E0369]: cannot add `{integer}` to `U8OrNothing`
--> src/chap4_optional.rs:9:12
|
9 | number + 1
| ------ ^ - {integer}
| |
| U8OrNothing
|
= note: an implementation of `std::ops::Add` might be missing for `U8OrNothing`
The error message is pretty clear: We can't add an integer to a value of type U8OrNothing. We thus have achieved our first goal: No more silent null values that we might forget to check for. The compiler forces us to check for the Nothing case!
Since this pattern ('I want either a value or nothing') is so common, it has a special name: This is an optional type. Rust has a built-in type called Option<T> for this: It encapsulates either a value of an arbitrary type T, or the special value None. The definition of the Option<T> type is very simple:
#![allow(unused)] fn main() { enum Option<T> { Some(T), None, } }
C++ also has a similar optional type, but not in the language itself, only in the standard library: std::optional<T>. Since C++ does not support pattern matching, it is arguably not as nice to use as Rust's Option<T> type.
With Option<T>, we could write a good log function that only returns an output when the input is greater than zero:
#![allow(unused)] fn main() { fn log2(num: f32) -> Option<f32> { if num <= 0.0 { None } else { Some(num.log2()) } } }
How optional types map to the hardware
As systems programmers, we want to know how we can map such a high-level construct onto our machine. In particular, we want our optional type to work as efficiently as possible! This is a fundamental principle of many systems programming languages: First and foremost, we want the ability to write code that is as efficient as possible, then we want our code to be nice and easy to write. Sometimes, it is possible to get both at the same time. C++'s creator Bjarne Stroustrup coined a term for an abstraction that is as efficient as a hand-rolled solution, but nicer to write: Zero-overhead abstraction. This is what we are looking for in systems programming: Abstractions that make it easier to write correct code (such as the Option<T> type in Rust), but are just as efficient if we had written the underlying mechanism by hand. So, what is the underlying mechanism making optional types possible?
Let's look back at the type sets that we analyzed previously, for example the set of valid values for the U8OrNone type: {0, 1, ..., 255, None}. When the compiler translates code using this type into machine code, it has to figure out how big this type is to allocate the appropriate amount of memory on the stack. Here is a neat trick: The minimum size of a type in bits is the base-2 logarithm of the magnitude of the set of values of this type, rounded up to the next integer:
\(sizeof(Type) = \lceil log_2 \lVert Type \rVert \rceil\).
Applying this formula to our U8OrNone type gives: \(sizeof(U8OrNone) = \lceil log_2 \lVert U8OrNone \rVert \rceil = \lceil log_2 257 \rceil = \lceil 8.0056 \rceil = 9 \). So we need 9 bits to represent values of the U8OrNone type, which intuitively makes sense: 8 bits for the numbers, and a single bit to indicate the absence of a number. Note that when the None bit is set, the value of the other bits don't matter: With 9 bits we can represent 512 different values, but we only need 257 values!
From here, we can see how we might implement our U8OrNone type in a language that does not support sum types natively: By adding a bit-flag that indicates the absence of a value:
#include <stdint.h>
#include <iostream>
#include <stdexcept>
struct U8OrNone {
U8OrNone() : _has_value(false) {}
explicit U8OrNone(uint8_t value) : _value(value), _has_value(true) {}
uint8_t get_value() const {
if(!_has_value) throw std::runtime_error{"Can't get_value() when value is None!"};
return _value;
}
bool has_value() const {
return _has_value;
}
private:
uint8_t _value;
bool _has_value;
};
int main() {
U8OrNone none;
U8OrNone some{42};
std::cout << "None: " << none.has_value() << std::endl;
std::cout << "Some: " << some.get_value() << std::endl;
// Note that there is no separate type here for `None`. We could
// still just do get_value() on `none` and it would be a bug that
// the compiler can't catch...
std::cout << none.get_value() << std::endl;
return 0;
}
Since the smallest addressable unit on most systems will be a single byte, the U8OrNone type will actually be two bytes instead of one byte (on x64 Linux using gcc 11). This might seem somewhat wasteful, but it is the best we can do in this scenario.
One thing worth debating is why we don't simply use the value 0 to indicate None. That way, we could store all values inside a single byte in our U8OrNone type. Think on this for a moment before reading on!
The problem is that the value 0 might be a perfectly reasonable value that users want to store inside the U8OrNone type. If you want to store the number of eggs in your fridge, 0 and None might be equivalent, but for an account balance for example, they might be different: An account balance of 0 simply indicates that there is no money in the account, but None would indicate that there is not even an account. These things are distinctly different!
Now, in some scenarios, the set of values of a type does contain a special type that indicates the absence of a value. This is exactly what the null value for pointers does! In these cases, we can use the special value to store our None value and safe some memory. This is called a null pointer optimization and Rust does this automatically! So Option<T> has the same size as T, if T is a pointer or reference type!
Exercise 4.2: Implement a simple optional type for C++ that can hold a single value on the heap through a pointer. What can you say about the relationship of this optional type and simple reference types in C++?
Using Option<T> in Rust
Option<T> is an immensely useful tool: It is everything that null is, but safer. Since it is one of the most fundamental types in Rust (besides the primitive types), we don't even have to include the Option<T> type from the standard library with a use statement, like we would have to do with other standard library files! Let's dig into how we can use Option<T>!
Option<T> has two variants: Some(T) and None. These can be used in Rust code like so:
#![allow(unused)] fn main() { let some = Some(42); let none : Option<i32> = None; }
Note that when using the None type, we might have to specify exactly what kind of Option<T> we want, as None fits any Option<T>! In many cases, the Rust compiler can figure the correct type out, but not always.
If we want to use the (potential) value inside an Option<T>, we have two options: We can either use a match statement, or we can use the unwrap function. match statements are the safer bet, as we will never run into the danger of trying to use the inner value of the Option<T> when it has no value, since we can't even access the value in the None arm of the match statement! Only if we are really 100% sure that there is a value, we can bypass the match statement and access the value directly using unwrap. If we try to call unwrap on an Option<T> that holds None, it will result in a panic, which in Rust will terminate the current thread (or your whole program if you panic on the main thread). Generally, panic is used whenever a Rust program encounters an unrecoverable condition. Trying to get the value of a None optional type is such a situation!
Take a look at the following example to familiarize yourself with the way Option<T> is used in Rust:
#![allow(unused)] fn main() { fn add_one_builtin(number: Option<u8>) -> Option<u8> { match number { Some(num) => Some(num + 1), None => None, } } fn add_one_builtin_verbose(number: Option<u8>) -> Option<u8> { if number.is_none() { None } else { let num = number.unwrap(); Some(num + 1) } } }
To figure out whether an Option<T> is Some(T) or None, we can also use the is_some and is_none functions. This is essentially the way option types work in C++, since C++ does not support the match syntax that Rust has.
This kind of operation right here - applying some transformation to the value contained within the Option<T>, but only if there is actually a value - is a very common pattern when using optional types. If we think of Option<T> as a boxJust a regular box. Not to be confused with the Rust Box<T>! Think cardboard, not heap! around a T, this is equivalent to unboxing the value (if it exists), performing the transformation, and putting the new value back into a box:
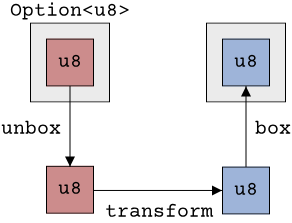
Notice from the picture that this transformation really can be anything. We don't have to add one, we could multiply by two, always return zero, as long as we take a value of type T and return some other value, this behaviour would work. We can even return something different, like turning a number into a string. So any function works, as long as it has the right input and output parameters. The set of input and output parameters to a function defines its type in RustRust is a bit simpler in that regard to C++, where functions can also be const or noexcept or can be member-functions, all of which contributes to the type of a function in C++.. So a function such as fn foo(val: i32) -> String has the type i32 -> String. The names of the parameters don't really matter, only their order and types. This syntax X -> Y is very common in functional programming languages, and it matches the Rust function syntax closely (which is no coincidence!), so we will use this syntax from now on. We can also talk about the signature of generic functions: The Rust function fn bar<T, U>(in: T) -> U has the signature T -> U.
Armed with this knowledge, we are now ready to bring Option<T> to the next level!
Higher-order functions
If we look at the add_one_builtin function from the previous example, we see that its type is Option<u8> -> Option<u8>. Now suppose that we instead had a function like this:
#![allow(unused)] fn main() { fn add_one_raw(num: u8) -> u8 { num + 1 } }
This function does the same thing as our add_one_builtin function, but on u8 values instead of Option<u8> values. The signature looks similar though: u8 -> u8. In our box-picture, here is where the function would sit:
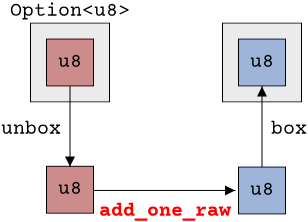
The interesting thing is that we could use any function of type u8 -> u8 here! The process of taking the value out of the box and putting the new value back into the box would be unaffected by our choice of function. So it would be annoying if we could not simply use our existing add_one_raw function with Option<u8> types. Why write a new function just to add the boilerplate of taking values out of the Option<u8> and putting them back in? We would have to do this every time we want to use some function with signature u8 -> u8 with Option<u8>. That would be a lot of unnecessary code duplication.
Luckily, Rust supports some concepts from the domain of functional programming. In particular, it is possible to pass functions as function arguments in Rust! So we can write a function that takes another function as its argument! So we could write a function that takes a value of type Option<u8> together with a function of type u8 -> u8 and only apply this function if the value is Some:
#![allow(unused)] fn main() { fn apply(value: Option<u8>, func: fn(u8) -> u8) -> Option<u8> { match value { Some(v) => Some(func(v)), None => None, } } }
In Rust, the type of a function u8 -> u8 is written as fn(u8) -> u8, so this is what we pass here. We then match on the value: If it is None, we simply return None, but if it is Some, we extract the value from the Some, call our function on this value and put the new value into another Some. We could say that we apply the function to the inner value, hence the name apply. We can now use this apply function to make existing functions work together with the Option<T> type:
fn add_one_raw(num: u8) -> u8 { num + 1 } fn mul_by_two(num: u8) -> u8 { num * 2 } pub fn main() { println!("{:?}", apply(Some(42), add_one_raw)); println!("{:?}", apply(Some(42), mul_by_two)); println!("{:?}", apply(None, add_one_raw)); }
This is perhaps one of the most powerful concepts that functional programming has to offer: Functions taking other functions as their arguments. We call such functions higher-order functions, and we will see a lot of those in the next chapters. Here is a picture that illustrates the process of apply visually:
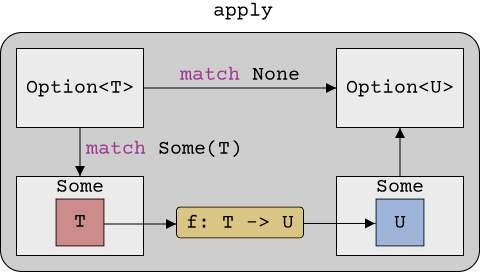
Of course, such a powerful function is already part of the Rust language: Option<T>::map. It is a bit more convenient to use, as it is a member function of the Option<T> type. The Rust documentation has a good example on how to use map:
#![allow(unused)] fn main() { let maybe_some_string = Some(String::from("Hello, World!")); let maybe_some_len = maybe_some_string.map(|s| s.len()); assert_eq!(maybe_some_len, Some(13)); }
Here, instead of using a named function (like we did with add_one_raw or mul_by_two), a closure is used, which is Rust's way of defining anonymous functions. Think of it as a short-hand syntax for defining functions. It is very handy together with higher-order functions like map that take other functions as arguments. Note that not every programming language allows passing functions around as if they were data. Earlier versions of Java for example did not allow this, which is why there you will see interfaces being passed to functions instead.
Besides map, which takes functions of type T -> U, there is also and_then, which takes functions that themselves can return optional values, so functions of type T -> Option<U>. Calling such a function with map would yield a return-value of type Option<Option<U>>, so a nested optional type. We often want to collapse these two Options into one, which is what and_then does.
Take some time to familiarize yourself with the API of Option<T>, as it is used frequently in Rust code!
Summary
In this chapter, we learned about the difference between product types and sum types and how we can use them to represent different sets of values. We learend that Rust has built-in support for sum types through the enum keyword, and that we can work with sum types using pattern matching using the match keyword. We learned how we can fairly easily fix the problems that null has by using a sum type called Option<T>. We also saw how sum types are represented on the hardware.
In the next section, we will build on this knowledge and look at another powerful abstraction: Iterators.