4.3. Algorithms
In this chapter, we will look at the many applications of iterators. Iterators are one of these abstractions that have found their way into basically all modern programming languages, simply because they are so powerful, making it easy to write maintainable code that clearly states its intent. The concepts of this chapter are equally well suited for systems programming and applications programming.
Algorithms give names to common tasks
Iterators are an abstraction for the concept of a range of values. Working with ranges is one of the most fundamental operations that we as programmers do. It turns out that many of the things that we want to do with a range of values are quite similar and can be broken down into a set of procedures that operate on one or more iterators. In the programming community, these procedures are often simply called algorithms, which of course is a label that fits to any kind of systematic procedure in computer science. In a sense, the algorithms on iterators are among the simplest algorithms imaginable, which is part of what makes them so powerful. They are like building blocks for more complex algorithms, and they all have memorable names that make it easy to identify and work with these algorithms. We will learn the names of many common algorithms in this chapter, for now let's look at a simple example:
pub fn main() { let numbers = vec![1,2,3,4]; for number in numbers.iter() { println!("{}", number); } }
This code takes an iterator to a range of values and prints each value to the standard output. A very simple program, and an example of the first algorithm: for_each. Rust has built-in support for the for_each algorithm using for loops, which is why perhaps this might not feel like an algorithm at all. We simply wrote a loop after all. And indeed, there is one step missing to promote this code to one of the fundamental algorithms on iterators. Algorithms on iterators are always about finding common behaviour in programs and extracting this behaviour into a function with a reasonable name. So let's write a more complicated function to see if we can find some common behaviour:
pub fn main() { let numbers = vec![2, 16, 24, 90]; for number in numbers.iter() { let mut divisor = 2; let mut remainder = *number; while remainder > 1 { if (remainder % divisor) == 0 { print!("{} ", divisor); remainder = remainder / divisor; } else { divisor += 1; } } println!(); } }
This piece of code prints all prime factors for each number in a range of numbers. Disregarding that the numbers are different, what has changed between this example and the previous example? We can look at the code side-by-side:
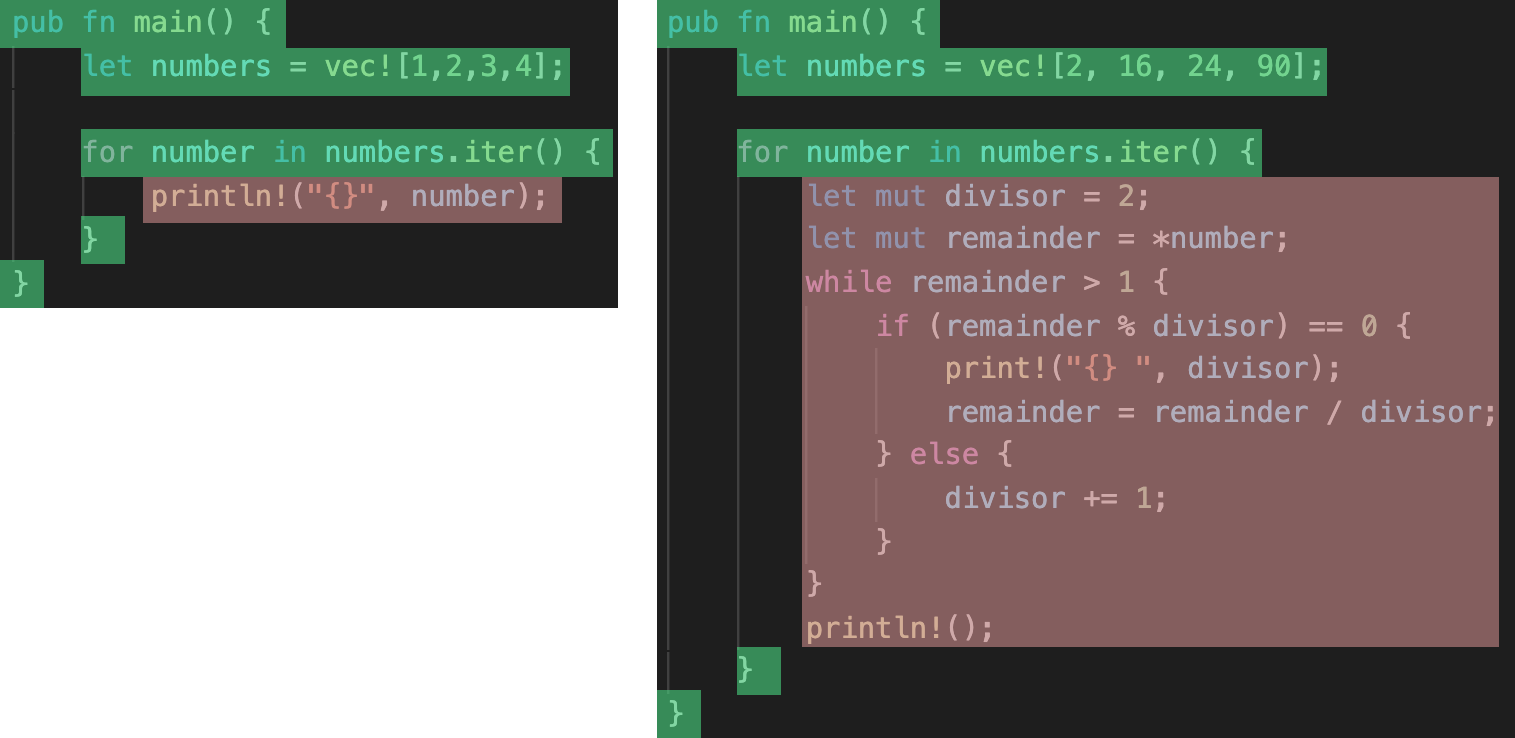
The only thing that is really different is the body of the loop. This is the operation that we want to apply for each value in the range. To clean up the loop in the second example, we could extract the loop body into a separate function print_prime_divisors:
fn print_prime_divisors(number: i32) { let mut divisor = 2; let mut remainder = number; while remainder > 1 { if (remainder % divisor) == 0 { print!("{} ", divisor); remainder = remainder / divisor; } else { divisor += 1; } } println!(); } pub fn main() { let numbers = vec![2, 16, 24, 90, 72, 81]; for number in numbers.iter() { print_prime_divisors(*number); } }
Now the two examples look very much alike, the only different is that one example uses the println! macro in the loop body and the other example calls the print_prime_divisors function. Now it becomes apparent what the idea of the for_each algorithm is: for_each applies a function to each element in a range! We could write a function named for_each that encapsulates all the common code of the last examples:
fn for_each<T, U: Iterator<Item = T>, F: Fn(T) -> ()>(iter: U, f: F) { for element in iter { f(element); } } pub fn main() { let numbers = vec![2, 16, 24, 90, 72, 81]; for_each(numbers.into_iter(), print_prime_divisors); }
The signature of the for_each function is a bit complicated, because of all the constraints that we have to enforce on our types. Let's try to unmangle it:
fn for_each<T is simple: A function that iterates over any possible value, hence the unconstrained type T. U: Iterator<Item = T> tells our function that it accepts any type U that implements the Iterator trait with the Item type set to T. This is Rusts way of saying: Any type that iterates over values of type T. Lastly, F: Fn(T) -> () encapsulates the function that we want to apply to each element in the range. Since this function has to be able to accept values of type T, we write Fn(T). We also don't care about a possible return value of the function (since it is discarded anyways), so we require that our function does not return anything: -> (). The function arguments then indicate a value of the iterator type U (iter: U) and a function (f: F).
We can call this for_each function with any iterator and matching function. We have to use into_iter() here, because the iterator returned from calling iter() on a Vec<i32> iterates over borrows to each element (&i32), but our print_prime_divisors function takes a number by value (i32). into_iter() instead returns an iterator that iterates over the raw values.
It is also possible to visualize the for_each algorithm schematically:
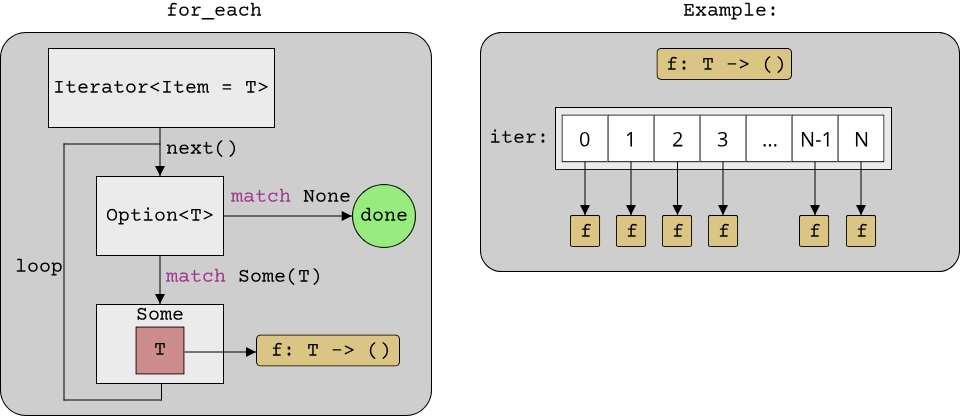
Now, we called our for_each function with two arguments: The iterator and the function to apply. Sometimes the function call syntax (a.b()) is easier to read, so it would be nice if we could apply to for_each function directly to a range: range.for_each(do_something). It turns out that this is rather easy when using stateful iterators as Rust does! If the iterator itself were to provide the for_each method, we could call it in such a way. We would have to provide for_each for all types that are iterators in Rust though. Luckily, all iterator types in Rust implement the Iterator trait, so into this trait is where the for_each method should go. Of course, Iterator already defines for_each (along with tons of other helpful methods that we will learn about shortly):
pub fn main() { let numbers = vec![2, 16, 24, 90, 72, 81]; numbers.into_iter().for_each(print_prime_divisors); }
The signature of Iterator::for_each is worth investigating:
fn for_each<F>(self, f: F) where F: FnMut(Self::Item)
Notice that it takes the self parameter by value, not as a mutable borrow as one might expect. This is because for_each consumes the iterator. Once we have iterated over all elements, we can't use the iterator anymore, so we have to make sure that no one can access the iterator after calling for_each. This is done by taking the self parameter by value, a neat trick that Rust allows to define functions that consume the value that they are called on.
You might have noticed that Rust is lacking the typical for loop that many other languages have, where you define some state, a loop condition and statements for updating the state in every loop iteration. for(int i = 0; i < 10; ++i) {} is not available in Rust. With iterators and for_each, we can achieve the same result, using a special piece of Rust syntax that enables us to create number-ranges on the fly:
pub fn main() { (0..10).for_each(|idx| { println!("{}", idx); }); // Which is equivalent to: for idx in 0..10 { println!("{}", idx); } }
The algorithms zoo
As mentioned, there are many algorithms in the fashion of for_each. In Rust, many interesting algorithms are defined on the Iterator trait, and even more can be found in the itertools crate. Even though C++ does not have a common base type for iterators, it also defines a series of algorithms as free functions which accept one or multiple iterator pairs. In C++, these algorithms reside in the <algorithm> header. It is also worth noting that C++ got an overhauled iterators and algorithms library with C++20, called the ranges library. The study of the ranges library is fascinating, as it enables many things that were lacking in the older algorithms, however in this lecture we will not go into great detail here and instead focus on the corresponding algorithms in Rust.
We will look at many specific algorithms on iterators in the next sections, but before we dive into them we will first look at a rough classification of the types of algorithms on iterators that we will encounter in Rust. For C++, there is already a nice classification by Jonathan Boccara called The World Map of C++ STL Algorithms, which is worth checking out. He groups the C++ algorithms into 7 distinct families and we will do something quite similar for the Rust algorithms on iterators.
Eager and lazy iteration
At the highest level, there are two types of algorithms: Eager algorithms and lazy algorithms. Since Rust iterators are stateful, we have to do something with them (i.e. call the next() function on them) so that computation happens. For iterators that point into a collection of elements, this distinction seems to be pedantic, but we already saw iterators that generate their elements on the fly, such as the C++ NumberRange iterator that we wrote in the last chapter, and the number-range syntax (0..10) in Rust. The actual computation that generates the elements happens at the moment of iteration, that is whenever we call next() on the iterator. We call an iterator that does not compute its results right away a lazy iterator, and an iterator that computes its elements before we ever use it an eager iterator. This distinction becomes important when the amount of work that the iterator has to perform grows. Think back to this example that we saw in the last chapter:
int sum(const std::vector<int>& numbers) {
int summand = 0;
for(size_t idx = 0; idx < numbers.size(); ++idx) {
summand += numbers[idx];
}
return summand;
}
Here we used a container to store numbers that we then wanted to sum. We later saw that we could achieve something similar with an iterator that generates the elements on the fly. Using a container that has to store all numbers before we actually calculate our sum is a form of eager iteration; using the NumberRange type that generates the numbers on the fly is an example of lazy iteration. In the limit, lazy iterators enable us to work with things that you wouldn't normally expect a computer to be able to handle, for example infinite ranges. The Rust number-range syntax enables us to define half-open ranges by only specifying the start number. This way, we can create an (almost) infinite range of numbers, far greater at least than we could keep in memory:
pub fn main() { for number in 2_u64.. { if !is_prime(number) { continue; } println!("{}", number); } }
The syntax 2_u64.. generates a lazy iterator that generates every number from 2 up to the maximum number that fits in a u64 value, which are about \(1.84*10^{19}\) numbers. If we were to store all those numbers eagerly, we would need \(8B*1.84*10^{19} \approx 1.47*10^{20}B = 128 EiB\) of memory. 128 Exbibytes of working memory, which is far beyond anything that a single computer can do today. At the moment of writing, the most powerful supercomputer in the world (Fugaku) has about 4.85 Petabytes of memory, which is less than a thousandth of what our number-range would need. With lazy iteration, we can achieve in a single line of code what the most powerful computer in the world can't achieve were we to use eager iteration.
Algorithms grouped into eager and lazy
Since Rust iterators are lazy, we have to evaluate them somehow so that we get access to the elements. A function that takes a lazy iterator and evaluates it is called an eager function. for_each is such an eager function, as it evaluates the iterator completely. Other examples include last (to get the last element of a range) or nth (to get the element at index N within the range). The fact that some algorithms are eager raises the question if all algorithms are eager. It turns out that many algorithms are not eager but lazy themselves, and that these lazy algorithms are among the most useful algorithms. But how can an algorithm be lazy?
Simply put, lazy algorithms are algorithms that take an iterator and return another iterator that adds some new behaviour to the initial iterator. This is best illustrated with an example. Rember back to our example for printing the prime factors for a range of numbers. Here we had a range of numbers (an iterator) and a function that calculated and printed the prime factors for any positive number. Wouldn't it be nice if we had an iterator that yielded not numbers themselves, but the prime factors of numbers? We could write such an iterator:
#![allow(unused)] fn main() { struct PrimeIterator<I: Iterator<Item = u64>> { source_iterator: I, } }
First, we define a new iterator PrimeIterator, which wraps around any Iterator that yields u64 values. Then, we have to implement Iterator for PrimeIterator:
#![allow(unused)] fn main() { impl <I: Iterator<Item = u64>> Iterator for PrimeIterator<I> { type Item = Vec<u64>; fn next(&mut self) -> Option<Self::Item> { self.source_iterator.next().map(get_prime_divisors) } } }
Our PrimeIterator will yield a Vec<u64>, which will contain all prime factors for a number. We can then take the code that we had for calculating and printing the prime divisors of a number and modify it so that it only calculates the prime divisors and stores them in a Vec<u64>. We can then use the map method of the Option<T> type that we already know to apply this new get_prime_divisors method to the result of a single iteration step of the source iterator. And that's it! We now have an iterator that yields prime factors:
fn main() { for prime_divisors in PrimeIterator::new(20..40) { println!("{:?}", prime_divisors); } }
Notice that the implementation of Iterator for our PrimeIterator was very simple. The only specific code in there was the Item type (Vec<u64>) and the function that we passed to map (get_prime_divisors). Notice that the Item type is actually defined by the return type of the get_prime_divisors function. If we could somehow 'extract' the return type of the function, we could make our PrimeIterator so generic that it could take any function with the signature u64 -> U. If we would then add a second generic parameter to the PrimeIterator type that defines the items of the source_iterator, we would end up with something like an adapter that can turn any Iterator<Item = T> into an Iterator<Item = U>, given a suitable function T -> U. Does this sound familiar to you?
This is exactly what the map function for Option<T> does, but for iterators! On Option<T>, map had the signature (Option<T>, T -> U) -> Option<U>, and we now defined a function (Iterator<Item = T>, T -> U) -> Iterator<Item = U>. It would make sense to name this function map as well. Lo and behold, the Iterator trait already defines this function: Iterator::map. Schematically, it looks almost identical to Option::map:
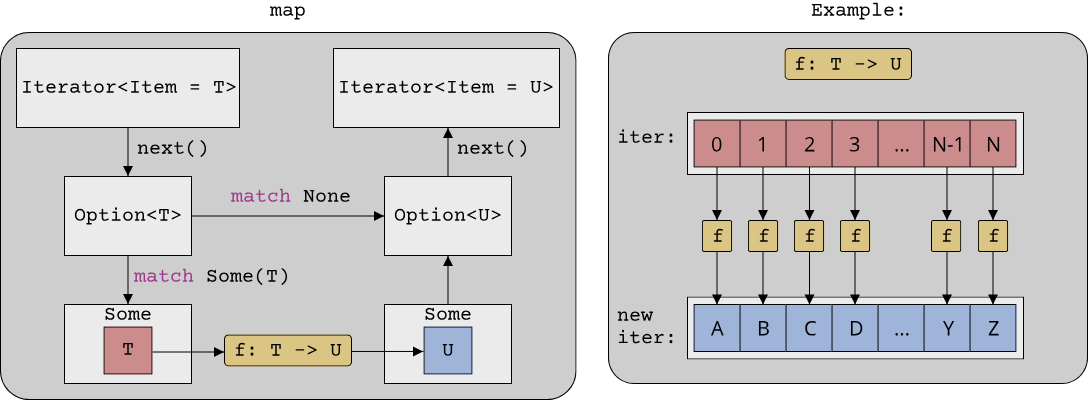
Compared to for_each, map is a lazy algorithm: It returns a new lazy iterator, the function T -> U is only called if this new iterator is evaluated (i.e. its elements are accessed by calling next). Besides map, there are many other lazy algorithms, such as filter, chain or enumerate. In the Rust standard library, these algorithms can be identified because they return new iterator types. map for example returns the special Map<I, F> iterator type.
Queries: The first specific group of algorithms
Now that we know about the difference between lazy and eager algorithms, we can look at the first group of useful algorithms called the query algorithms. Wikipedia defines a query as a precise request for information retrieval, which describes the query algorithms quite well. A query algorithm can be used to answer questions about a range of elements.
A quick primer on predicate functions
The question to ask is typically encoded in a so-called predicate function, which is a function with the signature T -> bool. The purpose of a predicate is to determine whether a value of type T is a valid answer for a specific question. In one of the examples in this chapter, we used a function fn is_prime(number: u64) -> bool to determine whether a specific u64 value is a prime number or not. is_prime is a predicate function! Predicate functions are often pure functions, which means that they have no side-effects. A pure function will give the same result when called repeatedly with the same arguments. is_prime(2) will always return true, so it is a pure function. Pure functions are nice because they are easy to understand and, since they have no side-effects, easy to handle in code. If we can encode a specific question with a predicate function and make it pure, we often end up with nice, readable, and safe code.
The actual query algorithms
These are the query algorithms that are available on the Iterator trait:
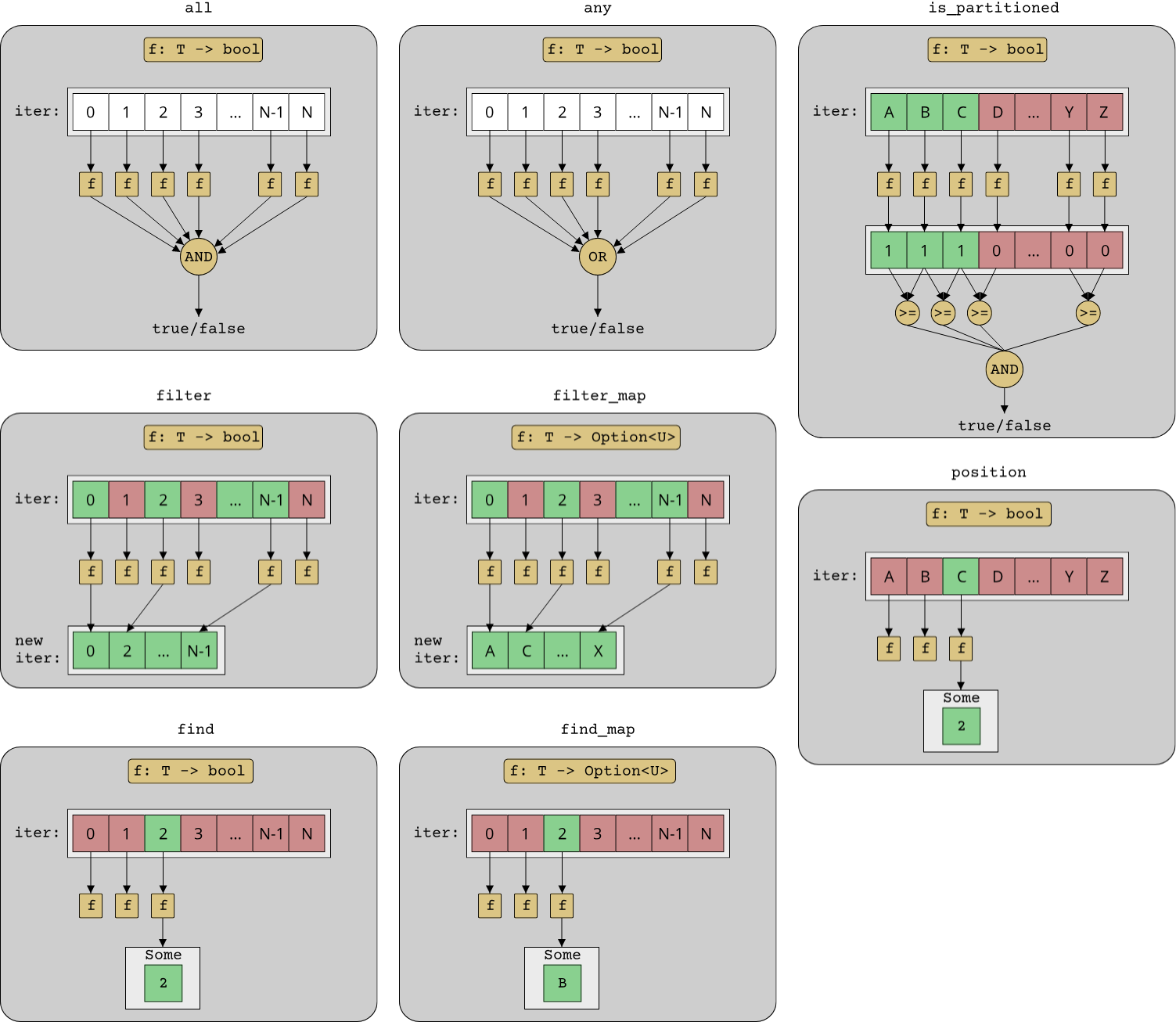
allwith the signature(Iterator<Item = T>, T -> bool) -> bool: Do all elements in the given range match the predicate?anywith the signature(Iterator<Item = T>, T -> bool) -> bool: Is there at least one element in the given range that matches the predicate?filterwith the signature(Iterator<Item = T>, T -> bool) -> Iterator<Item = T>: Returns a new iterator which only yields the elements in the original iterator that match the predicate.filter_mapwith the signature(Iterator<Item = T>, T -> Option<U>) -> Iterator<Item = U>: Combinesfilterandmap, returning only the elements in the original iterator for which the predicate returnsSome(U).findwith the signature(Iterator<Item = T>, T -> bool) -> Option<T>: Returns the first element in the original iterator that matches the predicate. Since there might be zero elements that match, it returnsOption<T>instead ofT.find_mapwith the signature(Iterator<Item = T>, T -> Option<U>) -> Option<U>: Likefilter_map, combinesfindandmap, returning the first element in the original iterator for which the predicate returnsSome(U), converted to the typeU.is_partitionedwith the signature(Iterator<Item = T>, T -> bool) -> bool: Returnstrueif the original range is partitioned according to the given predicate, which means that all elements that match the predicate precede all those that don't match the predicate. There are also variants for checking if a range is sorted (is_sorted,is_sorted_by,is_sorted_by_key).positionwith the signature(Iterator<Item = T>, T -> bool) -> Option<usize>: Likefindbut returns the index of the first matching element. For getting the index from the back, there is alsorposition.
The following image illustrates all query algorithms schematically:
Evaluators: The next group of algorithms
The next group of algorithms has no real name, but we can group all algorithms that evaluate a whole range or part of it into one category that we will call the evaluators. Here are all the evaluators:
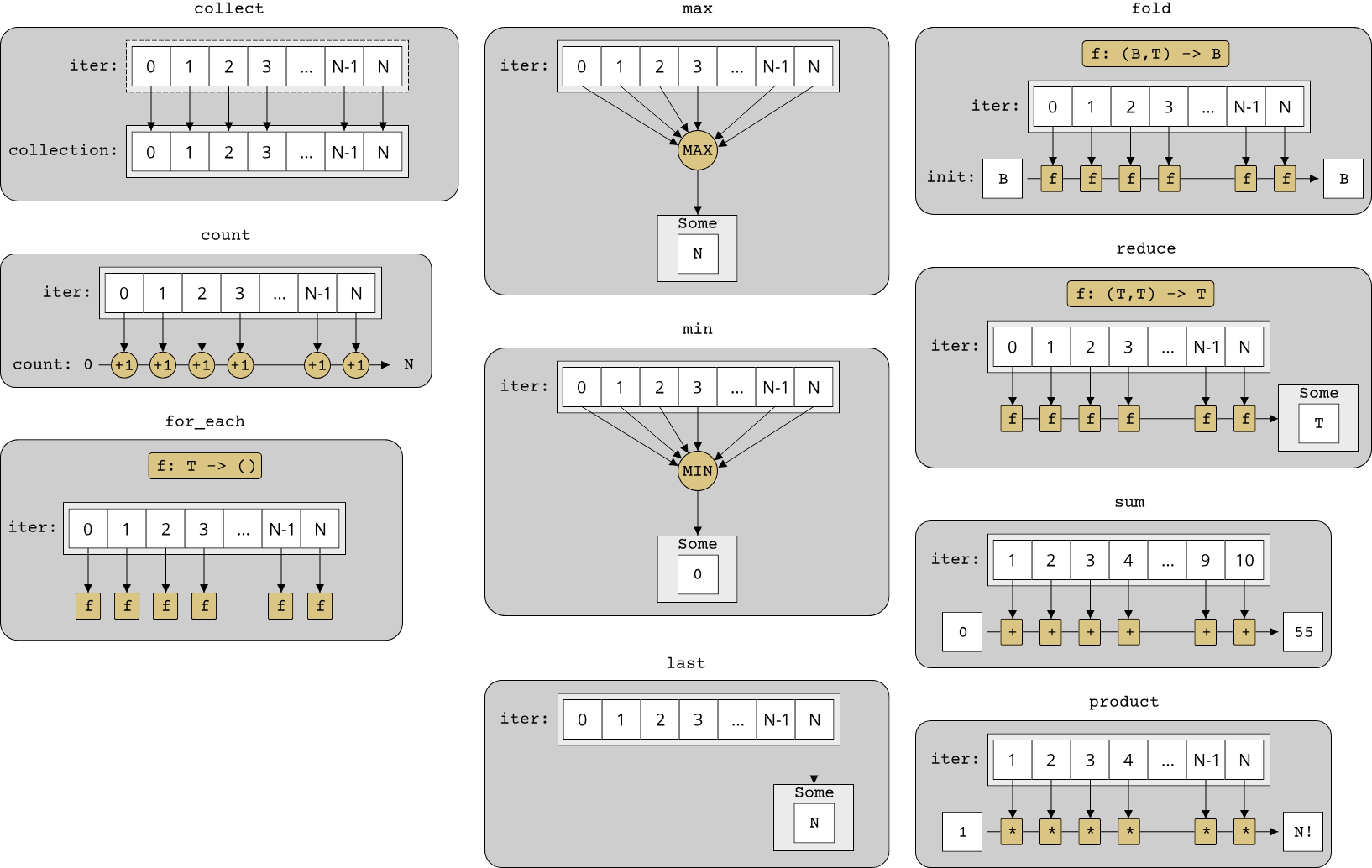
collectwith the signatureIterator<Item = T> -> B, whereBis any kind of collectionThis is a simplification. The more detailed answer is thatBis any type that implements theFromIteratortrait, which is a trait that abstractions the notion of initializing a collection from a range of elements. If you have an iterator and want to put all its elements into a collection, you can implementFromIteratoron the collection and put the relevant code on how to add the elements to the collection into this implementation. Then, you can either use thecollectfunction on theIteratortrait, or useYourCollection::from_iterator(iter).: This is perhaps the most common iterator function that you will see, as it allows collecting all elements from an iterator into a collection. As an example, if you have an iterator and want to put all its elements into aVec<T>, you can writelet vec: Vec<_> = iter.collect();.countwith the signatureIterator<Item = T> -> usize: Evaluates the iterator, callingnextuntil the iterator is at the end, and then returns only the number of elements that the iterator yielded.foldwith the signature(Iterator<Item = T>, B, (B, T) -> B) -> B. This signature is quite complicated and consists of three parts: The iterator itself, an initial value of an arbitrary typeB, and a function that combines a value of typeBwith an element from the iterator into a new value of typeB.foldapplies this function to every element that the iterator yields, thus effectively merging (or folding) all values into a single value.foldis quite abstract, but a very common use-case forfoldis to calculate the sum of all numbers in a range, in which case the initial value is0and the function to combine two values is simply+.for_eachwith the signature(Iterator<Item = T>, T -> ()) -> (), which we already know.lastwith the signatureIterator<Item = T> -> Option<T>. This evaluates the iterator until the end and returns the last element that the iterator yielded. Since the iterator might already be at the end, the return type isOption<T>instead ofT.maxandminwith the signatureIterator<Item = T> -> Option<T>. This evaluates the iterator until the end and returns the maximum/minimum element that the iterator yielded. Just aslast, since the iterator might already be at the end, the return type isOption<T>instead ofT. These functions use the default orderThe default order of a typeTin Rust is given by its implementation of theOrdorPartialOrdtrait. This is Rust's abstraction for comparing two values for their relative order.Ordis for all types that form a total order,PartialOrdfor all types that form a partial order. of the typeT, if you want to get the maximum/minimum element by another criterion, there are alsomin_by/max_byandmin_by_key/max_by_key. The first variant takes a custom function to compare two values, the second variant takes a function that converts fromTto some other typeUand uses the default order ofU.productwith the signatureIterator<Item = T> -> PwherePis the result type of multiplying two values of typeTwith each other. This is a special variant offoldfor multiplying all values in a range with each other. For numerical types, it is equivalent to callingfoldwith initial value1and*as the function.reducewith the signature(Iterator<Item = T>, (T, T) -> T) -> Option<T>. This is a variant offoldthat does not take an initial parameter and does not support transforming the elements of the iterator to another type.sumwith the signatureIterator<Item = T> -> SwhereSis the result type of adding two values of typeTto each other. This is a special variant offoldfor adding all values in a range to each other. For numerical types, it is equivalent to callingfoldwith initial value0and+as the function.
Where the query algorithms extracted information from parts of a range, most of the evaluators evaluate all elements in the range and do something with them. Knowing only collect and for_each from this category of algorithms is already sufficient for many applications, but it also pays off to understand fold, which is one of the most powerful algorithms there are. As we saw, there are several specific variants of fold, and the fact that seemingly fundamental operations such as sum and product are actually specializations of the fold algorithm should give you an idea of the power of fold. fold is one of the favorite tools of many functional programmers, as it can make code quite elegant, but for people not used to fold it can also make the code harder to read, so that is something to be aware of.
Here are all the evaluators visualized:
The transformations: The third group of algorithms
The third group of algorithms is all about transforming the way an iterator behaves. We already saw some variants of this group when we examined the query algorithms, namely filter_map and find_map, which are variants of the map algorithm that we already know. With iterators, there are two things that we can transform: The item type of an iterator, or the way the iterator steps through its range. map belongs to the first category, an algorithm that reverses the order of an iterator would belong to the second category.
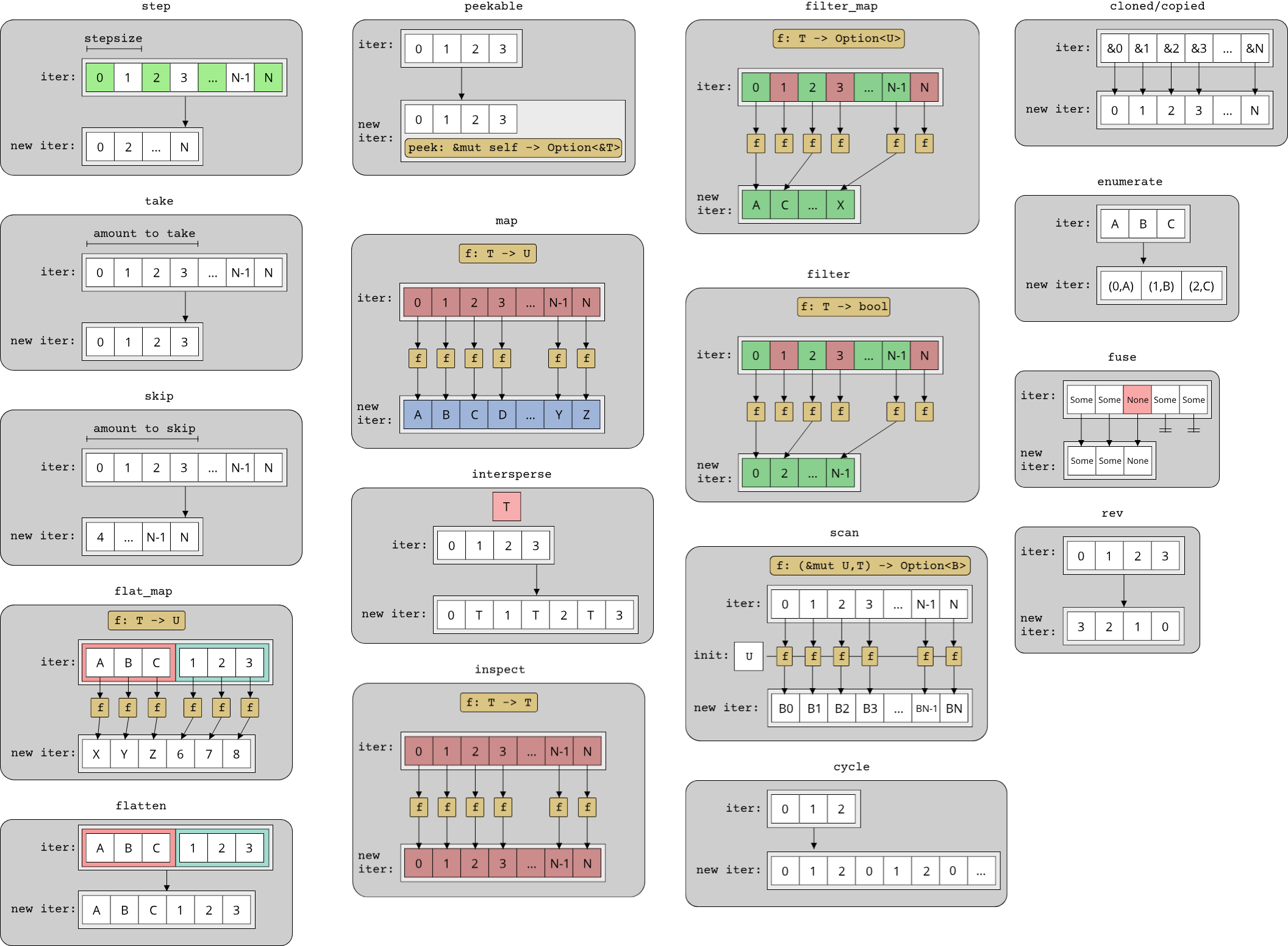
Here are all the transformations:
clonedwith the signatureIterator<Item = &T> -> Iterator<Item = T>. For an iterator over borrows, this returns a new iterator that instead returnscloned values of the item typeT. As the Rust documentation states:This is useful when you have an iterator over &T, but you need an iterator over T.copiedwith the signatureIterator<Item = &T> -> Iterator<Item = T>. This is identical toclonedbut returns copies instead of clones. Whereclonedonly required that the typeTimplementsClone,copiedrequires thatTimplementsCopy. SinceCopyallows potentially more efficient bit-wise copies,copiedcan be more efficient thancloned.cyclewith the signatureIterator<Item = T> -> Iterator<Item = T>. This returns a new iterator that starts again from the beginning once the initial iterator has reached the end, and will do so forever.enumeratewith the signatureIterator<Item = T> -> Iterator<Item = (usize, T)>. This very useful algorithm returns a new iterator that returns the index of each element together with the element itself, as a pair(usize, T).filterandfilter_mapalso belong to this category, because they change the behaviour of the iterator. As we already saw those in an earlier section, they are not explained again.flattenwith the signatureIterator<Item = Iterator<Item = T>> -> Iterator<Item = T>: Flattens a range of ranges into a single range. This is useful if you have nested ranges and want to iterate over all elements of the inner ranges at once.flat_mapwith the signature(Iterator<Item = T>, T -> U) -> Iterator<Item = U>, whereUis any type that implementsIntoIterator: This is a combination ofmapandflattenand is useful if you have amapfunction that returns a range. Only calling map on an iterator with such a function would yield a range of ranges,flat_mapyields a single range over all inner elements.fusewith the signatureIterator<Item = T> -> Iterator<Item = T>: To understandfuse, one has to understand a special requirement for iterators in Rust, namely that they are not required to always returnNoneon successive calls tonextif the first call returnedNone. This means that an iterator can temporarily signal that it is at the end, but upon a future call tonext, it is perfectly valid that the same iterator can returnSome(T)again. To prevent this behaviour,fusecan be used.inspectwith the signature(Iterator<Item = T>, T -> T) -> Iterator<Item = T>: Allows you to inspect what is going on during iteration by adding a function that gets called for every element in the iterator during iteration. This is similar tofor_each, howeverfor_eacheagerly evaluated the iterator, whereasinspectreturns a new iterator that will lazily call the given function.interspersewith the signature(Iterator<Item = T>, T) -> Iterator<Item = T>: Allows you to add a specific value between any two adjacent values in the original iterator. So a range like[1, 2, 3]with a call tointersperse(42)becomes[1, 42, 2, 42, 3]. If you want to generate the separator on the fly from a function, you can useintersperse_with.map, which we already know. There is alsomap_while, which takes a map function that might returnNoneand only yields elements as long as this function is returningSome(T).peekablewith the signatureIterator<Item = T> -> Peekable<Item = T>: Adds the ability to peek items without advancing the iterator.revwith the signatureIterator<Item = T> -> Iterator<Item = T>: Reverses the direction of the given iteratorscanwith the signature(Iterator<Item = T>, U, (&mut U, T) -> Option<B>) -> Iterator<Item = Option<B>>: This is the lazy variant offoldskipwith the signature(Iterator<Item = T>, usize) -> Iterator<Item = T>: This is the lazy variant ofadvance_by. If you want to skip elements as long as they match a predicate, you can useskip_whilewhich takes a predicate function instead of a count.stepwith the signature(Iterator<Item = T>, usize) -> Iterator<Item = T>: Returns an iterator that steps the given amount in every iteration. Every iterator by default has a step-size of 1, so e.g. if you want to iterate over every second element, you would usestep(2).takewith the signature(Iterator<Item = T>, usize) -> Iterator<Item = T>: Returns an iterator over the firstNelements of the given iterator. IfNis larger than or equal to the number of elements in the source iterator, this does nothing. Like withskip, there is alsotake_whilewhich returns elements as long as they match a predicate. The difference tofilteris that bothskip_whileandtake_whilestop checking the predicate after the first element that does not match the predicate, whereasfilterapplies the predicate to all elements in the range.
As you can see, there are a lot of transformation algorithms available on the Iterator trait. Arguably the most important ones are the filter and map variants, enumerate, skip, and take, as you will see those most often in Rust code.
Here are all the transformations visualized:
The groupings
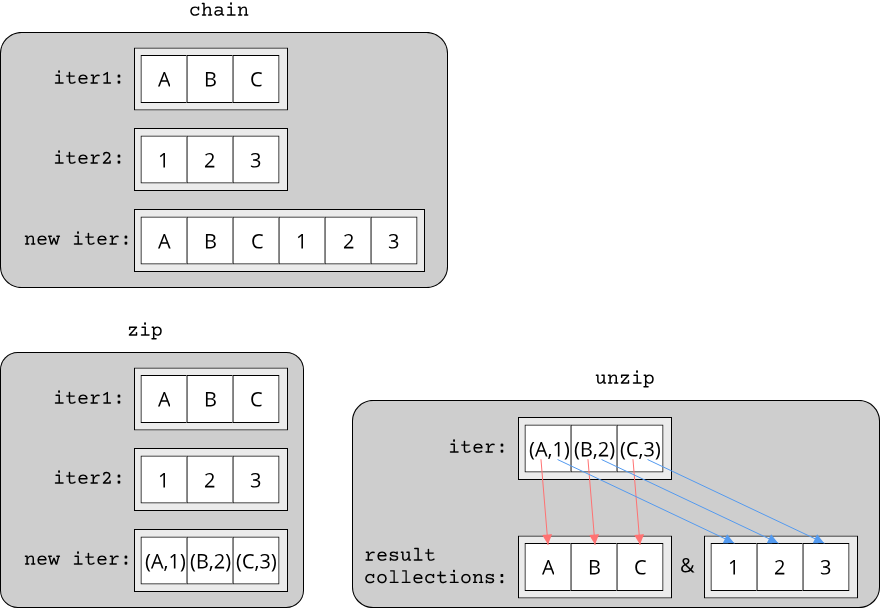
The next category of algorithms is all about grouping multiple ranges together:
chainwith the signature(Iterator<Item = T>, Iterator<Item = T>) -> Iterator<Item = T>: It puts the second iterator after the first iterator and returns a new iterator which iterates over both original iterators in succession. This is useful if you want to treat two iterators as one.zipwith the signature(Iterator<Item = T>, Iterator<Item = U>) -> Iterator<Item = (T, U)>: Just like a zipper,zipjoins two iterators into a single iterator over pairs of elements. If the two iterators have different lengths, the resulting iterator will be as long as the shorter of the two input iterators.zipis very useful if you want to pair elements from two distinct ranges.unzipwith the signatureIterator<Item = (T, U)> -> (Collection<T>, Collection<U>): This is the reverse ofzip, which separates an iterator over pairs of elements into two distinct collections, where one collection contains all first elements of the pairs and the other collection all second elements of the pairs.
The grouping algorithms are useful to know when you have multiple ranges that you want to treat as a single range. It is sometimes possible to create clever solutions for certain problems using zip.
Here are the groupings visualized:
The orderings
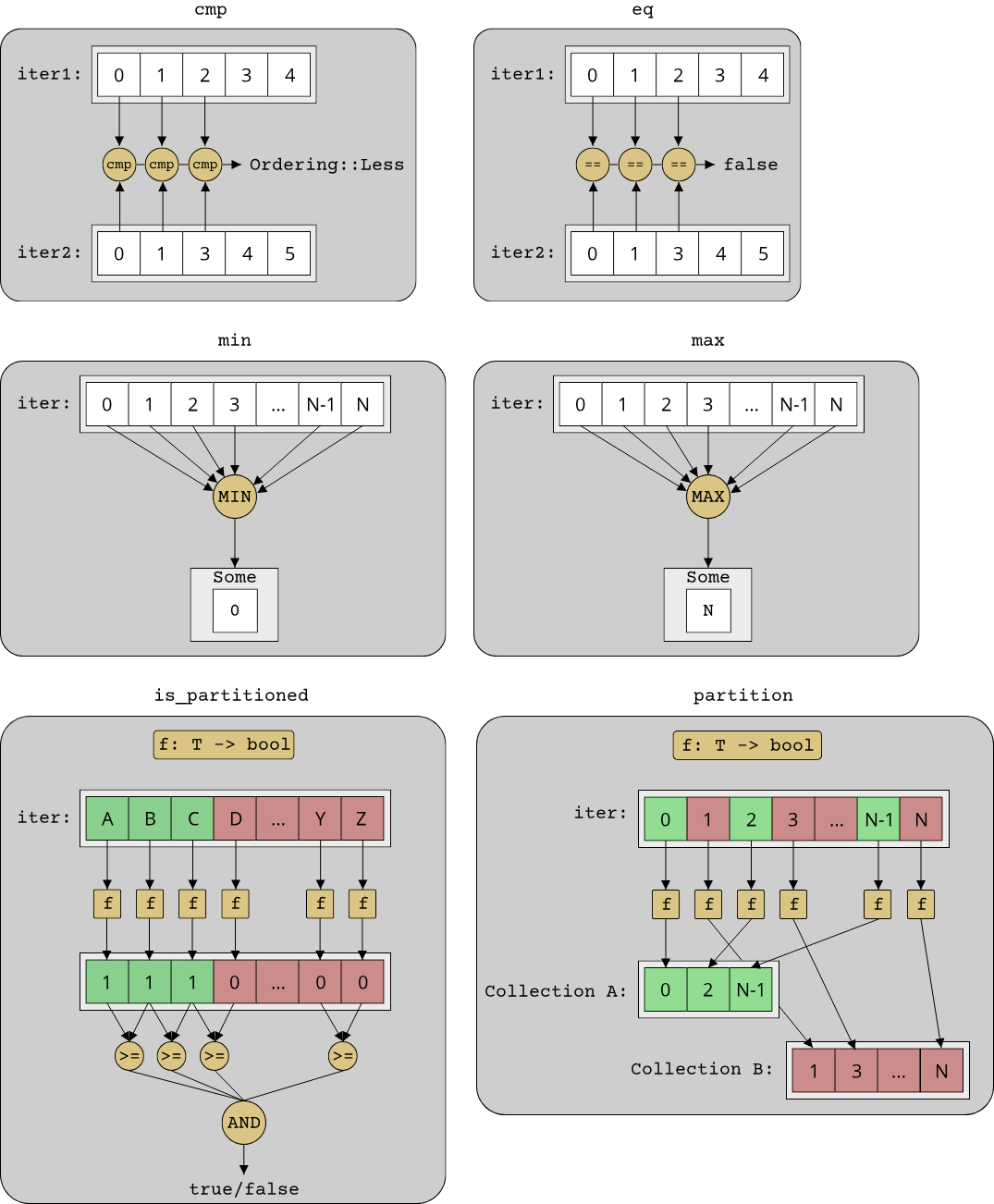
The last category of algorithms is all about the order of elements. There are a bunch of functions to compare two iterators based on their elements, as well as one function that changes the order of elements:
cmpwith the signature(Iterator<Item = T>, Iterator<Item = T>) -> Ordering: Performs a lexicographic comparison of the elements of both iterators. The definition for what exactly a lexicographic comparison entails can be found in the Rust documentation. If you don't want to use the default ordering of the elements, you can usecmp_byto specify a custom comparison function. For typesTthat only define a partial order,partial_cmpandpartial_cmp_bycan be used.- For all possible orderings (
A < B,A <= B,A == B,A != B,A >= B, andA > B), there are functions that check this ordering for any two iterators with the same type:lt,le,eq,ne,ge, andgt.eqalso has aeq_byvariant that takes a custom comparison function. is_partitionedand theis_sortedvariants also belong to this category of algorithms.maxandminand their variants also belong to this category of algorithms.partitionwith the signature(Iterator<Item = T>, T -> bool) -> (Collection<T>, Collection<T>): Partitions the range of the given iterator into two collections, with the first collection containing all elements which match the predicate and the second collection containing all elements which don't match the predicate. There is also an experimentalpartition_in_placewhich reorders the elements in-place without allocating any memory.
Here are all the orderings visualized (excluding the variants of cmp and eq):
Upon seeing this list, a reasonable question to ask is if there is a sort algorithm. The answer is that there is no sort for iterators in Rust. Sorting is what is known as an offline algorithm, which is the technical term for an algorithm that requires all data at once. Intuitively, this makes sense: The element that should be put at the first position after sorting might be the last element in the original range, so any sorting algorithm has to wait until the very end of the range to identify the smallest element. But Rust iterators are lazy, so they don't have all elements available up-front. It is for this reason that it is impossible to write a sort function that works with an arbitrary iterator. Instead, sort is implemented on the collections that support sorting, such as Vec<T> or LinkedList<T>.
Why we should prefer algorithms over for-loops
Algorithms on iterators are very useful because they make code a lot more readable. They do this by giving names to common patterns in our code. In particular, they help us to untangle loops, since most loops actually perform the same action as one or multiple of these algorithms. Here are some examples:
#![allow(unused)] fn main() { // This is `filter`: for element in collection.iter() { if condition(element) { continue; } // Do stuff } // This is `map`: for element in collection.iter() { let data = element.member; // or let data = func(element); // Do stuff } // This is `find`: let mut result = None; for element in collection.iter() { if condition(element) { result = Some(element); break; } } }
In the C++-world, the usage of algorithms is actively taught by many professionals in the industry, as many talks indicate. The main reason is that C++ traditionally was close to C, and in C raw for-loops were often the way to go. In the Rust-world, for-loops play a lesser role and hence using algorithms on iterators comes more naturally here. For both languages, algorithms on iterators are often the preferred way to write code that deals with ranges, since they are in many cases easier to understand than an equivalent for-loop.
When not to use algorithms
Of course there is no silver bullet in programming, and algorithms are certainly no exception to this rule. While it is often a good idea to use these algorithms instead of a regular for-loop, algorithms do have some downsides. Perhaps the biggest downside is that they can make debugging hard, because they hide a lot of code in the internal implementation of the algorithm functions (map, filter, for_each). Since these functions are part of the standard library, they tend to be more complicated than one might expect, due to certain edge cases and general robustness requirements for library functions. When trying to debug code that makes heavy use of these algorithms, it can be hard to find suitable code locations to add breakpoints, and a lot of the state that might be interesting for debugging will often be located in a different function or be hidden somewhat, compared to a regular for-loop.
The second downside to using algorithms is that they are not always the best solution in terms of readability. If you are wrestling a lot to get some piece of code to work with an algorithm because of this one weird edge case where you have to skip over one item but only if you observed some other item two steps before and instead you have to terminate after five items and.... Then it might just be better to use a regular loop with some comments. Particularily once one gets the hang of algorithms, it can become quite addictive to see how one can turn all possible loops into multiple algorithm calls.
Summary
In this chapter we learned about algorithms on iterators, which are small building blocks for common programming patterns when working with ranges of elements. We learned how to use the Iterator trait in Rust, which provides all sorts of useful functions, such as for_each, filter, or map. We also learned about the difference between eager and lazy iteration, and how lazy iteration even enables us to work with (almost) infinite ranges.
This chapter is meant as much as an introduction to algorithms as it is a reference for all the common algorithms that Rust provides. The visual representation of all agorithms might just help you in understanding an algorithm that you have seen in other code but didn't quite grasp.
This concludes chapter 4, which was all about zero-overhead abstractions. We learned about optional types and iterators, which are the bread and butter of programming in Rust. With this, we have a solid foundation to look at more specific aspects of systems programming, starting with error handling in the next chapter.